Competitive programming is a thrilling blend of problem-solving, algorithms, and data structures. Data structures are fundamental tools that allow us to store and organize data efficiently. In this blog, we'll explore the most commonly used data structures in competitive programming and how they can help you solve problems effectively.
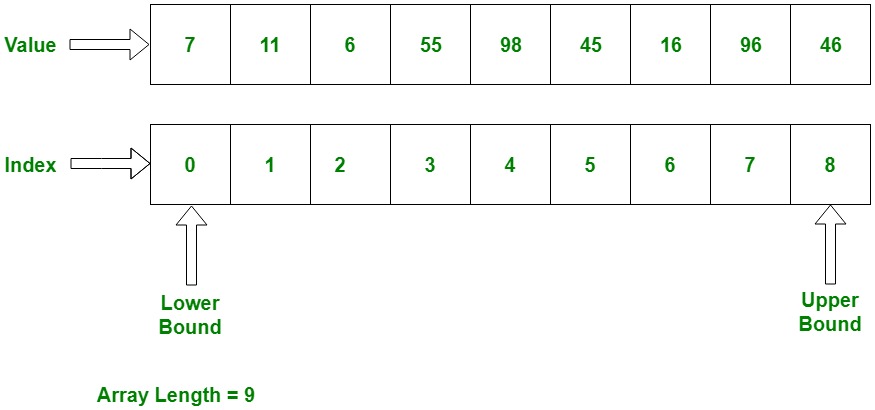
Arrays are the simplest and most commonly used data structure. They store elements in a contiguous block of memory. You can access any element in constant time O(1), making arrays ideal for problems where you need fast read/write access.
#include <iostream>
using namespace std;
int main() {
int arr[] = {2, 5, 1, 8, 3};
int n = sizeof(arr) / sizeof(arr[0]);
int maxElement = arr[0];
for (int i = 1; i < n; ++i) {
if (arr[i] > maxElement) {
maxElement = arr[i];
}
}
cout << "Maximum Element: " << maxElement << endl;
return 0;
}
A linked list consists of nodes where each node contains a data field and a reference to the next node. Linked lists are useful when you need to dynamically manage data, especially when the size of the data set can change frequently.
#include <iostream>
using namespace std;
struct Node {
int data;
Node* next;
};
void push(Node** head_ref, int new_data) {
Node* new_node = new Node();
new_node->data = new_data;
new_node->next = *head_ref;
*head_ref = new_node;
}
void printList(Node* node) {
while (node != NULL) {
cout << node->data << " ";
node = node->next;
}
}
int main() {
Node* head = NULL;
push(&head, 1);
push(&head, 2);
push(&head, 3);
cout << "Linked List: ";
printList(head);
return 0;
}
A stack is a LIFO (Last In, First Out) data structure. Elements are added and removed from the top. Stacks are useful for problems involving recursion, expression evaluation, and backtracking.
#include <iostream>
#include <stack>
using namespace std;
bool areParenthesesBalanced(string expr) {
stack<char> s;
for (char& ch : expr) {
if (ch == '(') {
s.push(ch);
} else if (ch == ')') {
if (s.empty()) return false;
s.pop();
}
}
return s.empty();
}
int main() {
string expr = "(())";
if (areParenthesesBalanced(expr)) {
cout << "Balanced" << endl;
} else {
cout << "Not Balanced" << endl;
}
return 0;
}A queue is a FIFO (First In, First Out) data structure. Elements are added at the rear and removed from the front. Queues are useful for problems involving order, such as breadth-first search (BFS).
#include <iostream>
#include <queue>
using namespace std;
int main() {
queue<int> q;
q.push(1);
q.push(2);
q.push(3);
cout << "Queue front: " << q.front() << endl;
q.pop();
cout << "Queue front after pop: " << q.front() << endl;
return 0;
}
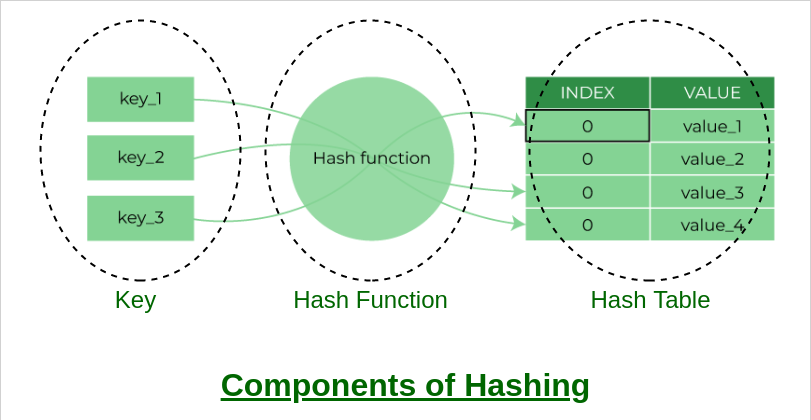
Hash tables provide average-case constant time complexity O(1) for insertion, deletion, and search operations. They are useful for problems where you need fast lookups.
#include <iostream>
#include <unordered_map>
using namespace std;
int main() {
int arr[] = {1, 2, 2, 3, 3, 3};
int n = sizeof(arr) / sizeof(arr[0]);
unordered_map<int, int> freq;
for (int i = 0; i < n; ++i) {
freq[arr[i]]++;
}
for (auto& pair : freq) {
cout << pair.first << ": " << pair.second << endl;
}
return 0;
}
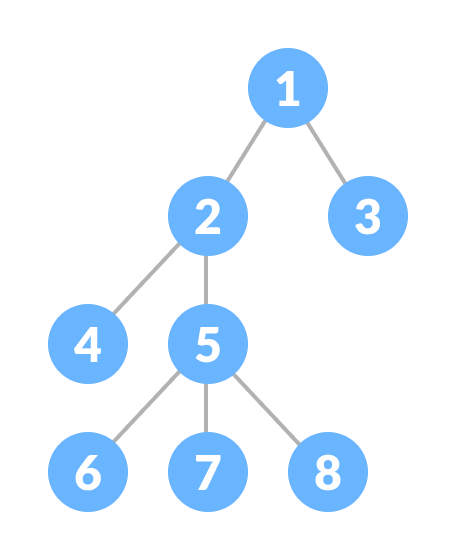
Trees are hierarchical data structures with a root node and children. Binary trees, binary search trees (BSTs), and AVL trees are commonly used types. Trees are useful for representing hierarchical data and for fast search, insert, and delete operations in balanced trees.
#include <iostream>
using namespace std;
struct Node {
int data;
Node* left;
Node* right;
};
Node* newNode(int data) {
Node* node = new Node();
node->data = data;
node->left = node->right = NULL;
return node;
}
void inorderTraversal(Node* root) {
if (root == NULL) return;
inorderTraversal(root->left);
cout << root->data << " ";
inorderTraversal(root->right);
}
int main() {
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "In-order traversal: ";
inorderTraversal(root);
return 0;
}
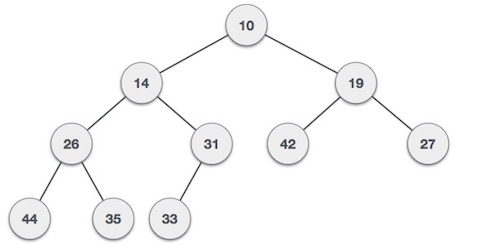
Heaps are specialized binary trees that satisfy the heap property. Min-heaps allow fast access to the smallest element, while max-heaps allow fast access to the largest. Heaps are useful for priority queues and for algorithms like heapsort.
#include <iostream>
#include <queue>
using namespace std;
int main() {
priority_queue<int, vector<int>, greater<int>> minHeap;
minHeap.push(3);
minHeap.push(1);
minHeap.push(2);
cout << "Min-Heap top: " << minHeap.top() << endl;
minHeap.pop();
cout << "Min-Heap top after pop: " << minHeap.top() << endl;
return 0;
}
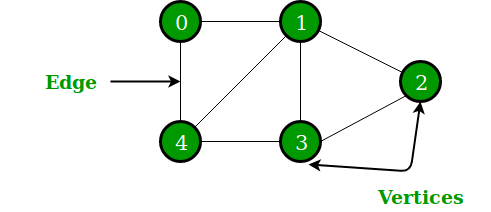
Graphs consist of nodes (vertices) and edges. They are used to represent networks and relationships. Graphs can be represented using adjacency matrices or adjacency lists. Common algorithms include depth-first search (DFS) and breadth-first search (BFS).
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
void BFS(int start, vector<vector<int>> &graph, vector<bool> &visited) {
queue<int> q;
q.push(start);
visited[start] = true;
while (!q.empty()) {
int node = q.front();
q.pop();
cout << node << " ";
for (int neighbor : graph[node]) {
if (!visited[neighbor]) {
q.push(neighbor);
visited[neighbor] = true;
}
}
}
}
int main() {
int n = 5; // Number of nodes
vector<vector<int>> graph(n);
graph[0] = {1, 2};
graph[1] = {0, 3, 4};
graph[2] = {0};
graph[3] = {1};
graph[4] = {1};
vector<bool> visited(n, false);
cout << "BFS starting from node 0: ";
BFS(0, graph, visited);
return 0;
}
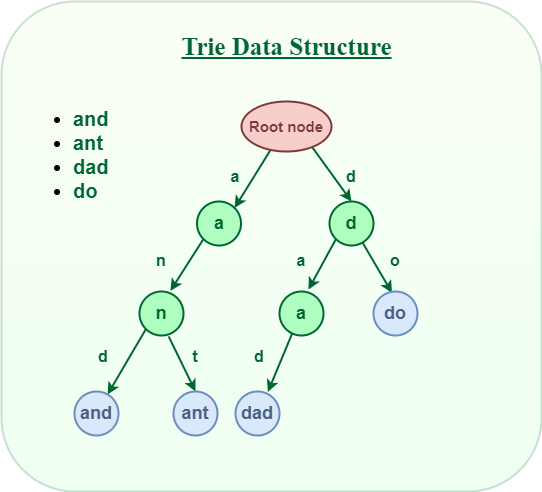
Tries, also known as prefix trees, are used to store strings. They provide efficient search operations, especially for prefix-based queries. Tries are commonly used in autocomplete and spell-checking applications.
#include <iostream>
#include <unordered_map>
using namespace std;
struct TrieNode {
unordered_map<char, TrieNode*> children;
bool isEndOfWord;
TrieNode() : isEndOfWord(false) {}
};
class Trie {
public:
TrieNode* root;
Trie() { root = new TrieNode(); }
void insert(string word) {
TrieNode* node = root;
for (char ch : word) {
if (!node->children[ch]) {
node->children[ch] = new TrieNode();
}
node = node->children[ch];
}
node->isEndOfWord = true;
}
bool search(string word) {
TrieNode* node = root;
for (char ch : word) {
if (!node->children[ch]) return false;
node = node->children[ch];
}
return node->isEndOfWord;
}
};
int main() {
Trie trie;
trie.insert("hello");
trie.insert("world");
cout << "Search for 'hello': " << (trie.search("hello") ? "Found" : "Not Found") << endl;
cout << "Search for 'helloo': " << (trie.search("helloo") ? "Found" : "Not Found") << endl;
return 0;
}
Segment trees are advanced data structures used for range queries and updates. They are particularly useful for problems involving cumulative frequency tables and interval trees.
#include <iostream>
using namespace std;
const int MAX = 1e5;
int segmentTree[4*MAX];
int arr[MAX];
void build(int node, int start, int end) {
if (start == end) {
segmentTree[node] = arr[start];
} else {
int mid = (start + end) / 2;
build(2*node, start, mid);
build(2*node+1, mid+1, end);
segmentTree[node] = segmentTree[2*node] + segmentTree[2*node+1];
}
}
int query(int node, int start, int end, int l, int r) {
if (r < start || end < l) return 0;
if (l <= start && end <= r) return segmentTree[node];
int mid = (start + end) / 2;
int p1 = query(2*node, start, mid, l, r);
int p2 = query(2*node+1, mid+1, end, l, r);
return p1 + p2;
}
void update(int node, int start, int end, int idx, int val) {
if (start == end) {
arr[idx] = val;
segmentTree[node] = val;
} else {
int mid = (start + end) / 2;
if (start <= idx && idx <= mid) {
update(2*node, start, mid, idx, val);
} else {
update(2*node+1, mid+1, end, idx, val);
}
segmentTree[node] = segmentTree[2*node] + segmentTree[2*node+1];
}
}
int main() {
int n = 5;
arr[0] = 1; arr[1] = 2; arr[2] = 3; arr[3] = 4; arr[4] = 5;
build(1, 0, n-1);
cout << "Sum of values in given range = " << query(1, 0, n-1, 1, 3) << endl;
update(1, 0, n-1, 2, 10);
cout << "Updated sum of values in given range = " << query(1, 0, n-1, 1, 3) << endl;
return 0;
}